Minimum Spanning Set Selection in Graph Kernels

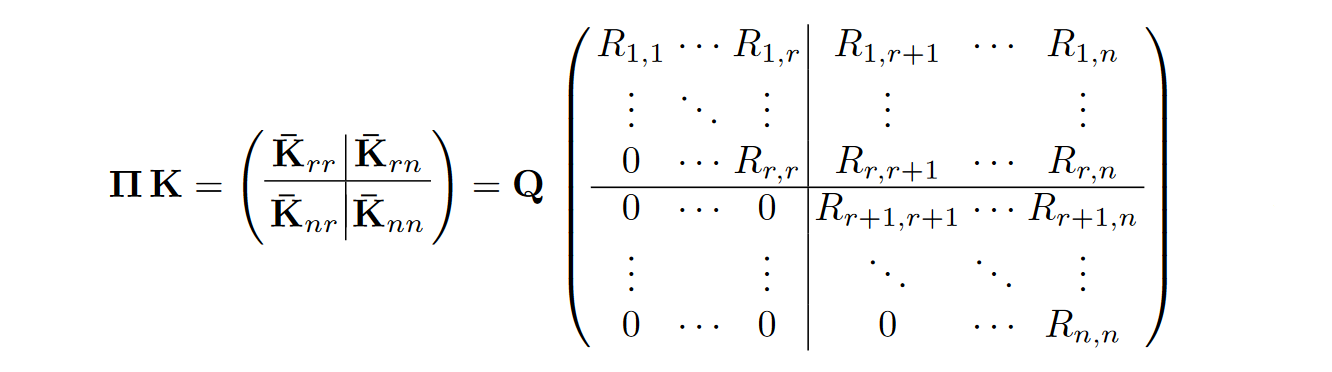
Kernel-based learning models such as support vector machines (SVMs) can seamlessly deal with graph structures thanks to suitable kernel functions that compute a particular similarity between pairs of data samples. In the last two decades, a plethora of graph kernels have been proposed, motivated by theoretical properties or designed specifically for an application domain. Computing graph kernels however presents a significant cost for both training and inference, since predictions on unseen graphs require evaluating the kernel e.g. between the new sample and all support vectors, and solutions to an SVM optimization problem are not guaranteed to be sparse. In this paper, we present a method to select a minimum set of spanning vectors for the solutions of SVMs, based on the rank-revealing QR decomposition of the kernel Gram matrix. We apply it on 18 real-world classification tasks on chemical compounds, showing its effectiveness to reduce the computational burden in performing inference on unseen graphs by minimizing the number of support vectors without penalizing accuracy. This in turn gives us a tool to better analyze the trade-off between accuracy, expressiveness and inference cost among different graph kernels.

Recommended citation: D. Tortorella, A. Micheli (2023). "Minimum Spanning Set Selection in Graph Kernels." Graph-Based Representations in Pattern Recognition. GbRPR 2023. LNCS vol. 14121, pp. 15-24.
Download Paper